HiGlassRM: Learning to Remove High-prescription Glasses via Synthetic Dataset Generation

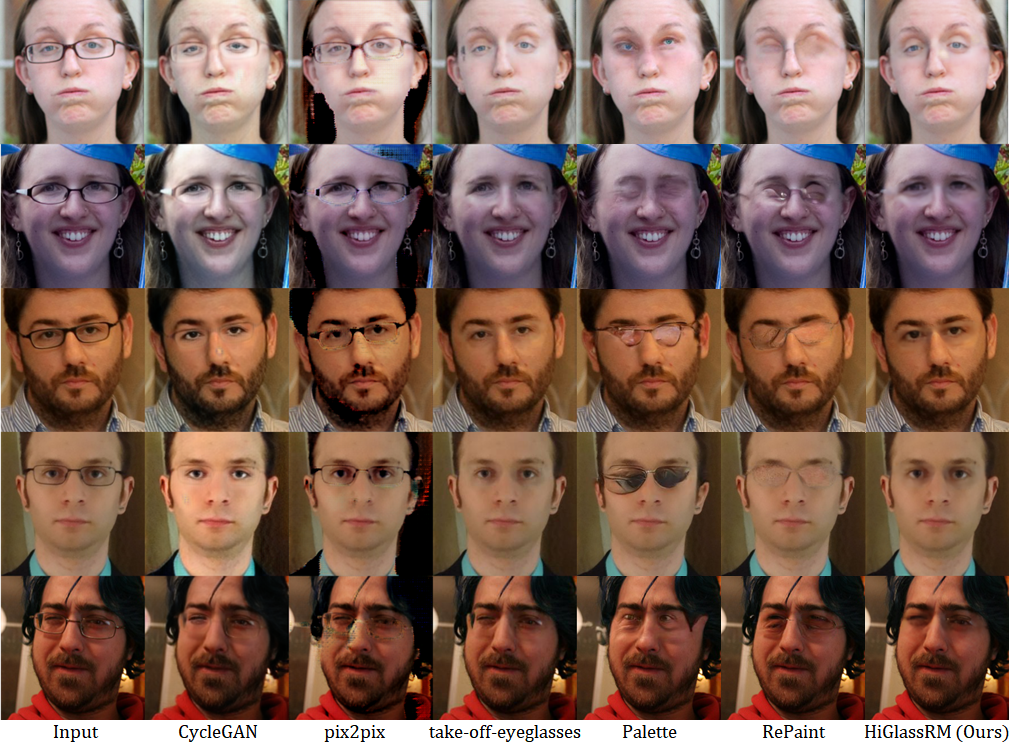
Figure1: Qualitative comparison on FFHQ [15]. Our HiGlassRM explicitly compensates this geometric distortion, preserving identity-consistent facial geometry and background alignment.overview

Abstract

Existing eyeglass removal methods can handle frames and shadows but fail to correct lens-induced geometric distortions, as public datasets lack the necessary supervision. To address this, we introduce the HiGlass Dataset, the first large-scale synthetic dataset providing explicit flow-based supervision for refractive warping. We also propose HiGlassRM, a novel pipeline whose core is a network that explicitly estimates a displacement flowmap to de-warp distorted facial geometry. Experiments on both synthetic and real images show that this flowmap-centric approach, trained on our data, significantly improves identity preservation and perceptual quality over existing methods. Our work demonstrates that explicitly modeling and correcting geometric distortion via flowmap estimation, enabled by targeted supervision, is key to faithful eyeglass removal.

HiGlass Dataset Overview

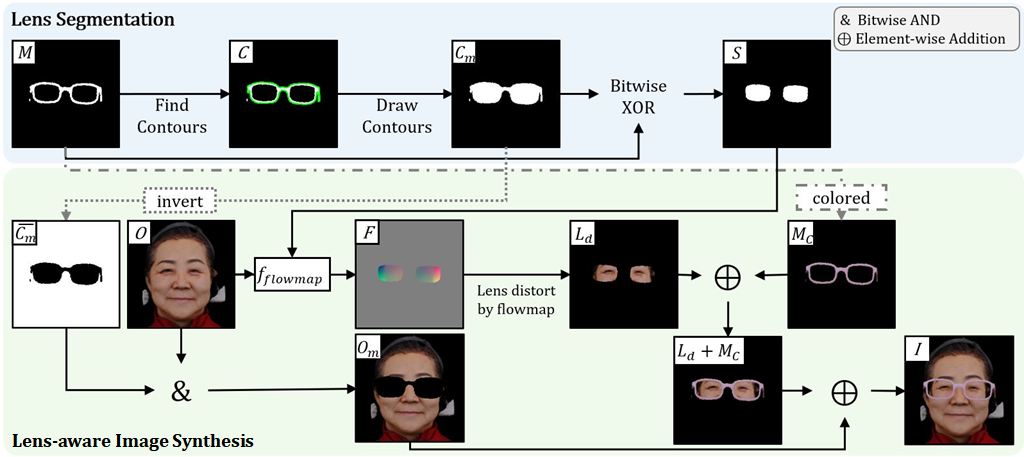Dataset Generation Overview Figure3: HiGlass Dataset synthesis overview

From the binary eyeglass-frame mask $M$, the outermost contour $C$ is detected and drawn to create the filled silhouette mask $C_m$. A bitwise XOR with $M$ yields the lens mask $S$. The complement $\overline{C}_m$ masks the face image $O$ to produce the background-preserved image $O_m$. A flow map $F$ is computed and applied inside $S$ to obtain the lens-distorted content $L_d$. Finally, the colored frame $M_C$ is added and the result is composited with $O_m$ to form the final image $I$.

Dataset Examples Figure6: Examples from HiGlass Dataset

The HiGlass Dataset provides rich visual samples showcasing diversity in frame shapes and lens powers. Each paired sample contains five core components: $(I, M, F, D, O)$. The HiGlass image $I$ is the final composite with all synthesized optical effects. The binary eyeglass-frame mask $M$ localizes only the frames. The displacement flowmap $F$ encodes the geometric warp caused by the lens (e.g., minification or magnification). The shadow-free image $D$ is a rendered variant that retains these optical effects but removes cast shadows. Finally, the face image $O$ is the eyeglass-free supervision target.

HiGlassRM Overview

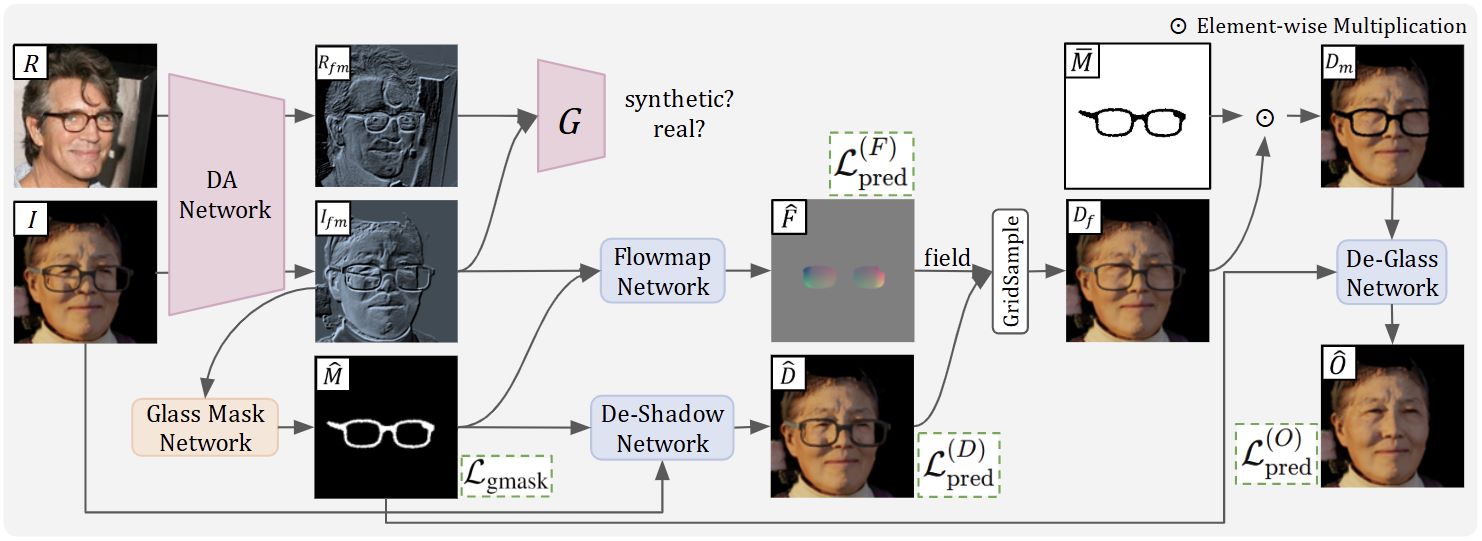Method Overview Figure4: Overview of the proposed HiGlassRM.

The framework begins by transforming the real image $R$ and synthetic image $I$ into unified feature maps $R_{fm}$ and $I_{fm}$ through the Domain Adaptation (DA) Network. The Glass Mask Network processes $I_{fm}$ to generate an eyeglass mask $\widehat{M}$, identifying the presence of eyeglasses. The De-Shadow Network takes $I$ and $\widehat{M}$ as input to produce a shadow-free image $\widehat{D}$. The Flowmap Network, using $I_{fm}$ and $\widehat{M}$, generates a flow map $\widehat{F}$ to correct distortion. This flow map is applied to $\widehat{D}$ through Grid Sampling, producing $D_f$. Next, element-wise multiplication with the inverted mask $\overline{M}$ yields the masked de-distorted image $D_m$. The De-Glass Network then processes $D_m$ and $\widehat{M}$ to generate the eyeglass-free image $\widehat{O}$.

Experimental Results on Real Data

Dataset Examples